The following formula gives the normal density function for a normally distributed variable:
f(x) = {1/(σ√2π)}exp{-(x-µ)2/(2σ2) } for -∞< x <+∞
The normal distribution function with mean, µ = 0 and standard deviation, σ = 1 is called the standard normal distribution or unit normal distribution.
The standardization of any normal distribution helps in comparison of that normal distribution to a standard normal distribution. To standardize a normally distributed random variable, we need to calculate its Z score. The Z-score is calculates using two steps: (1) The mean of X is subtracted from X (2) Then divided that by the standard deviation of X. All possible observations are adjusted using this procedure to achieve a standard normal random variable, Z.
Z = (X-µ)/σ
The advantage of standardization is that now we can get the results by viewing the standard normal distributed table. An extract from the table for the cumulative distribution function of the standard normal random variable is given below:
|
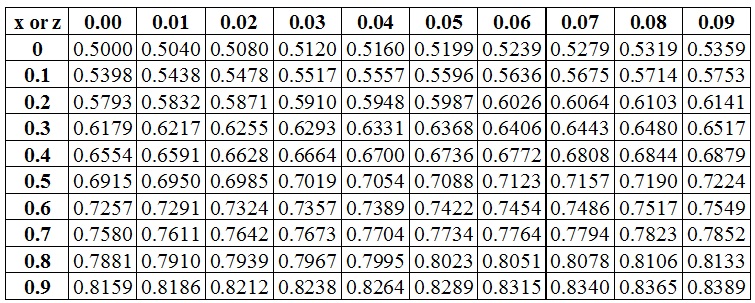
Table P(Z≤x) = N(x) for x≥0 or (Z≤z) = N(z) for z≥0
|
Another extract from the table is given below for the negative z values.
|
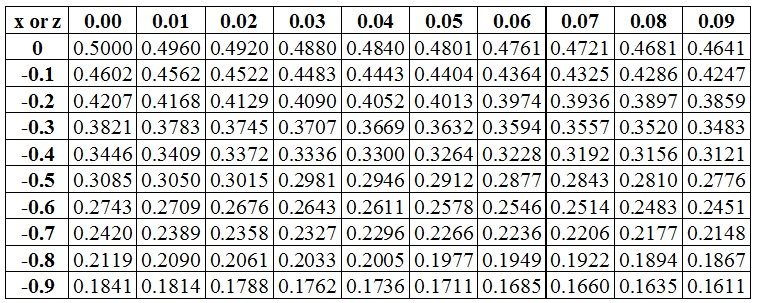
Table P(Z≤x) = N(x) for x≤0 or (Z≤z) = N(z) for z≤0
|
Reading cumulative standard normally distributed table: You should be comfortable in reading the values from the table. In the exam, you may get an extract from the table in the exam which has to be used to solve the problem.
The tables provide the cumulative probabilities for a standard normal distribution. For all the observations we need to calculate the z values. If the z value is zero that means that the observation is at the center and equal to mean. If the z value is plus one that means that the observation equals mean plus one standard deviation. If the z value is minus two, that means that the observation equals mean minus two standard deviations.
Since the table provides the cumulative probabilities, the positive z values will have more probability than the negative z values. The z value of zero has a cumulative probability of 0.50 i.e. it lies in the middle. For z=0.5, the table shows the value as 0.6915. It means that 69.15 percent of the times, the value will be equal to or lower than that observation value. We know that for z=0, the cumulative probability is 0.50. So, 19.15 percent of values lies between z=0 and z=0.5. Since the distribution is symmetric about the mean, it means that 19.15 percent of values also lies between z=0 and z=-0.5. So, the cumulative probability of z=-0.5 will be equal to 0.5 - 0.1915 = 0.3085 because the cumulative probability tells us the area on the left side of the observation. So, the area for z=-0.5 will be the area for z=0 minus the area between z=0 and z=-0.5. We can even confirm our answer from the cumulative probability table provided for negative z values.
You should be comfortable with calculating the required probability using either of the tables.
Also, z(x) + z(-x) = 1 because the area of the left of z(-x) will be equal to the area on the right side of z(x) because of symmetric distribution and thus the summation of these two will cover the entire area.
So, we can use the below formula as well to calculate the z values.
z(-x) = 1 - z(x)
|
Example 6: Calculating the probabilities using standard normal distribution
|
|
The annual returns on a stock are following a normal distribution. The expected value of the annual return is 12 percent with an annual standard deviation of 15 percent. Compute the following:
(a) the probability that the return will be positive
(b) the probability that the return will be lesser than 15 percent
(c) the probability that the return will lie between 8 percent to 18 percent
Solution:
Here, µ = 12 percent and σ = 15 percent
(a) The z value for zero return = (0 - 12)/15 = -0.80.
Here, we need to find the probability that the return is greater than zero percent. So, the area will lie on the right side of this z-value. The area of the right side of z=-0.80 will be equal to the one minus area of the left side of z=-0.80.
From the table, we get the area on the left side of -0.80 = 0.2119
So, the area of the right side of -0.80 = 1- 0.2119 = 0.7881.
Hence, the probability that the return will be positive is 78.81 percent.
(b) The z-value for 15 percent return = (15-12)/15 = 0.20
Here, we need to find the area on the left side of 0.20, and that will be given by the cumulative probability distribution from the table.
For z=0.2, the area is 0.5793.
Hence, the probability that the return will be lower than 15 percent is 57.93 percent.
(c) The z-value for 8 percent return = (8-12)/15 = -0.266
The z-value for 18 percent return = (18-12)/15 = 0.40
We need to find the area between these two z values to get our answer.
The area on the left of z=-0.26 is 0.3974 and the area on the left of z = -0.27 is 0.3936. So, the area on the left of z=-0.26666 will be equal to 0.3936 + (1/3)*(0.3974 - 0.3936) = 0.3974 - (2/3)(0.3974 - 0.3936) = 0.3949.
So, the area from z=-0.26 to z=0 will be equal to 0.5 - 0.3949 = 0.1051 because the area on the left of z=0 is 0.5.
The area on the left of z=0.4 is equal to 0.6554. So, the area between z=0.4 and z=0 will be equal to 0.6554 - 0.50 = 0.1554 because the area on the left of z=0 is 0.5.
So, the area between z=-0.266 and z=0.40 is equal to the sum of the area between z=-0.266 and z=0 and the area between z=0 and z=0.4.
The area between z=.266 and z-0.40 is equal to 0.1051 + 0.1554 = 0.2605.
Hence, the probability that the return will lie between 8 percent and 18 percent is 26.05 percent.
|
Previous LOS: Probability of a normally distributed random variable inside a given interval
Next LOS: Shortfall risk, safety-first ratio, and Roy's safety-first criterion


